Solid Modeling Techniques
The various methods for representing the solids are:
1. Half-space method
2. Boundary representation method (B-rep)
3. Constructive solid geometry (CSG and C-rep)
4. Sweep representation
5. Analytical solid modeling (ASM)
6. Primitive instancing
7. Spatial partitioning representation
a. Cell decomposition
b. Spatial occupancy enumeration
c. Octree encoding
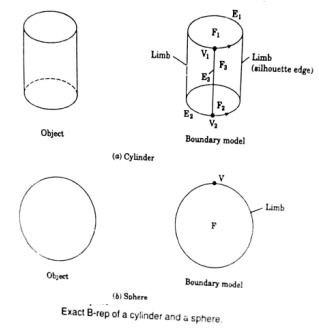
Boundary representation method (B-rep)
![]()
The main topological items / primitives of b-rep are:
In solid modeling and computer-aided design, boundary representation often abbreviated as B-rep or BREP—is a method for representing shapes using the limits.
A solid is represented as a collection of connected surface elements, the boundary between solid and non-so lid.
Boundary representation models are composed of two parts:
O Topology, and
O Geometry (surfaces, curves and points).
Vertex (V) : It is a unique point (an ordered triplet) in space
Edge (E): It is finite, non-self intersecting, directed space c urve bounded by t wo vertices that are not necessarily distinct
Face (F) : It is defined as a finite connected, non-self-intersecting, region of a closed oriented surface bounded by one or more loops
Loop (L) : It is an ordered alternating sequence of vertices and edges
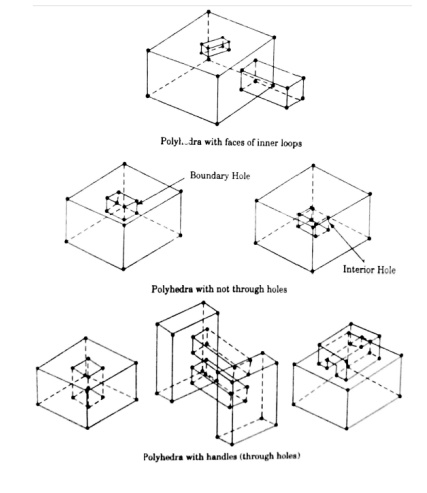
Genus (G) : It is the topological name for the number of handles or through holes in an object
Body/Shell(B) : It is a set of faces that bound a single connected closed volume. A minimum body is a point
A minimum body is a point; topologically this body has one face, one vertex, and no edges. It is called asemin al or singular body.
Geometry
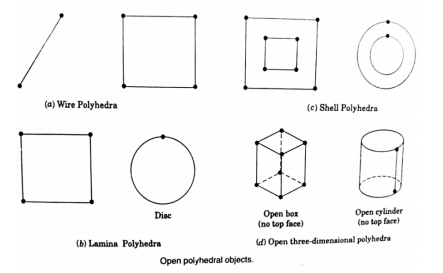
Open polyhedral objects
Curved Objects
Euler’s formula
Euler – Poinc are Law for closed objects : F – E + V – L = 2 (B – G)
Euler – Poinc are Law for open objects : F – E + V – L = B – G

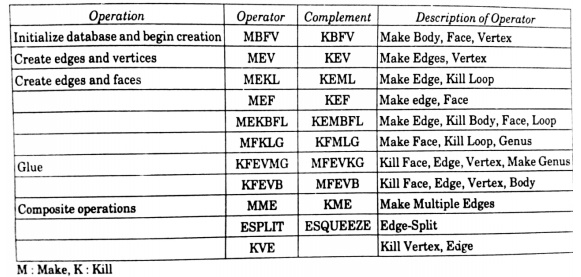
Some Euler Operations
Solid Model Generation using B-rep
Advantages of b-rep
O Appropriate to construct solid models of unusual shapes
O Relatively simple to c onvert a b-rep model to wireframe model
Disadvantages of b-rep
O Requires more storage
O Not suitable for applications like tool path generation
O Slow manipulation
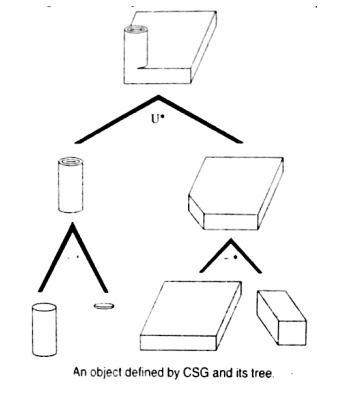
Constructive Solid Geometry (CSG and C-rep)
Constructive solid geometry (CSG) (formerly called computational binary solid geometry) is a techni que used in solid modeling.
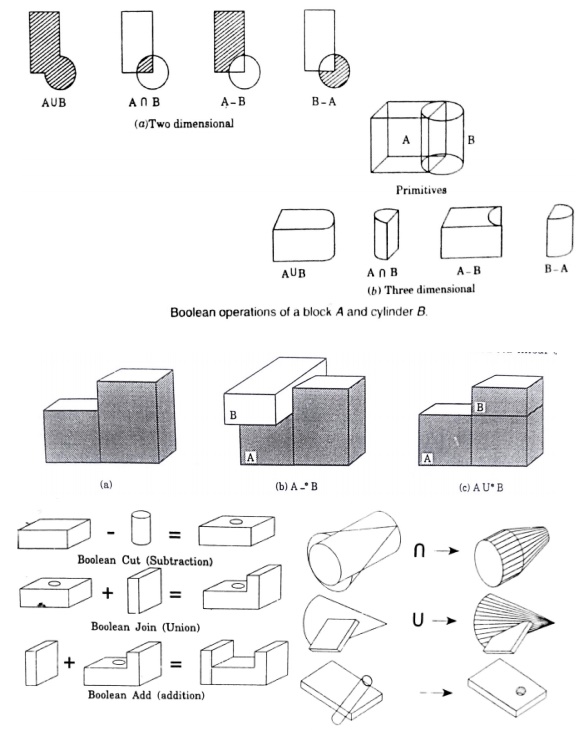
Constructive solid ge ometry allows a modeler to create a complex surface or object by using Boolean ope rators to combine objects.
Often CSG presents a model or surface that appears visually comple x, but is actually little more than cleve rly combined or de-combined objects
The simplest solid objects used for the representation are c alled primitives.
Typically they are the objects of simple shape:
O cuboids
O cylinders
O prisms
O pyramids
O spheres
O cones
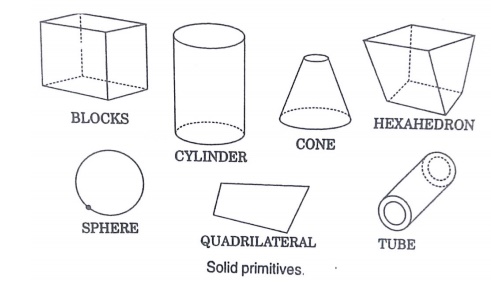
The set of allowable primitives is limited by each software packag e. Some software packages allow CSG on curved objects while other packages do not
It is said that an object is constructed from primitives by means of allowable operations , which are typically Boolean o perations on sets: union, intersection an d difference, as well as geometric transformati ons of those sets
Boolean Operations
CSG Tree