CONDUCTION WITH INTERNAL HEAT GENERATION:
Applications: current carrying conductor, chemically reacting systems, nuclear reactors. Energy generated per unit volume is given by V Eq.
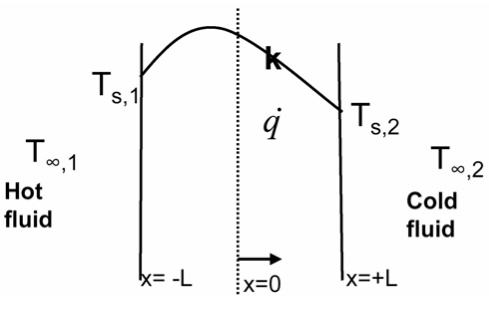
Plane wall with heat source: Assumptions: 1D, steady state, constant k, uniform
Consider one-dimensional, steady-state conduction in a plane wall of constant k, with uniform generation, and asymmetric surface conditions: Heat diffusion equation.
A medium through which heat is conducted may involve the conversion of mechanical, electrical, nuclear, or chemical energy into heat (or thermal energy).In heat conduction analysis, such conversion processes are characterized as heat generation.
For example, the temperature of a resistance wire rises rapidly when electric current passes through it as a result of the electrical energy being converted to heat at a rate of I2R, where I is the current and R is the electrical resistance of the wire The safe and effective removal of this heataway from the sites of heat generation (the electronic circuits) is the subject of electronics cooling, which is one of the modern application areas of heat transfer.
Likewise, a large amount of heat is generated in the fuel elements of nuclear reactors as a result of nuclear fission that serves as the heat source for the nuclear power plants. The natural disintegration of radioactive elements in nuclear waste or other radioactive material also results in the generation of heat throughout the body. The heat generated in the sun as a result of the fusion of hydrogen into helium makes the sun a large nuclear reactor that supplies heatto the earth.
Another source of heat generation in a medium is exothermic chemical reactions that may occur throughout the medium. The chemical reaction in this case serves as a heat source for the medium. In the case of endothermic reactions, however, heat is absorbed instead of being released during reaction, and thus the chemical reaction serves as a heat sink. The heat generation term becomes
a negative quantity in this case.
Often it is also convenient to model the absorption of radiation such as solar energy or gamma rays as heat generation when these rays penetrate deep into the body while being absorbed gradually. For example, the absorption of solar energy in large bodies of water can be treated as heat generation throughout the water at a rate equal to the rate of absorption, which varies with depth. But the absorption of solar energy by an opaque body occurs within a few microns of the surface, and the solar energy that penetrates into the medium in this case can be treated as specified heat flux on the surface.
Note that heat generation is a volumetric phenomenon. That is, it occurs throughout the body of a medium. Therefore, the rate of heat generation in a medium is usually specified per unit volume.
The rate of heat generation in a medium may vary with time as well as position within the medium. When the variation of heat generation with position is known, the total rate of heat generation in a medium of volume V can be determined from In the special case of uniform heat generation, as in the case of electric resistance heating throughout a homogeneous material, the relation in
reduces to E ·gen _ e · genV, where Egen is the constant rate of heat generation per unit volume.

