Dimensionless Parameters and their Significance
The following dimensionless parameters are significent in evaluating the convection heat transfer coefficient:
(a) The Nusselt Number (Nu)-It is a dimensionless quantity defined as hL/ k, where h = convective heat transfer coefficient, L is the characteristic length and k is the thermal conductivity of the fluid The Nusselt number could be interpreted physically as the ratio of the temperature gradient in the fluid immediately in contact with the surface to a reference temperature gradient (Ts - T inf) /L. The convective heat transfer coefficient can easily be obtained if the Nusselt number, the thermal conductivity of the fluid in that temperature range and the characteristic dimension of the object is known.
Let us consider a hot flat plate (temperature Tw) placed in a free stream (temperature T
inf< Tw). The temperature distribution is shown ill Fig. 2.4. Newton's Law of Cooling says that the rate of heat transfer per unit area by convection is given by
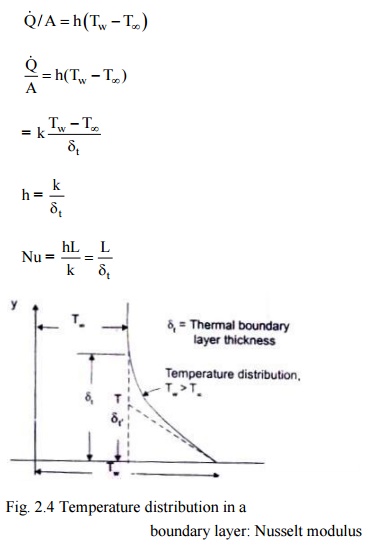
Fig. 2.4 Temperature distribution in a boundary layer: Nusselt modulus
The heat transfer by convection involves conduction and mixing motion of fluid particles. At the solid fluid interface (y = 0), the heat flows by conduction only, and is given by

Since the magnitude of the temperature gradient in the fluid will remain the same, irrespective of the reference temperature, we can write dT = d(T - Tw) and by introducing a characteristic length dimension L to indicate the geometry of the object from which the heat flows, we get
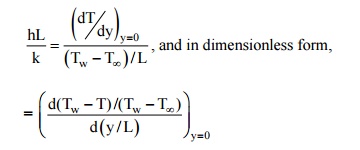
(b) The Grashof Number (Gr)-In natural or free convection heat transfer, die motion of fluid particles is created due to buoyancy effects. The driving force for fluid motion is the body force arising from the temperature gradient. If a body with a constant wall temperature Tw is exposed to a qui scent ambient fluid at T inf , the force per unit volume can be written as
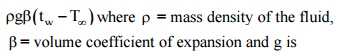
the acceleration due to gravity.
The ratio of inertia force × Buoyancy force/(viscous force)2 can be written as

The magnitude of Grashof number indicates whether the flow is laminar or turbulent. If the Grashof number is greater than 109, the flow is turbulent and for Grashof number less than 108, the flow is laminar. For 108 < Gr < 109, It is the transition range.
(c) The Prandtl Number (Pr) - It is a dimensionless parameter defined as Pr = mCp / k =/n a
where mis the dynamic viscosity of the fluid, v = kinematic viscosity and a = thermal diffusivity.
This number assumes significance when both momentum and energy are propagated through the system. It is a physical parameter depending upon the properties of the medium It is a measure of the relative magnitudes of momentum and thermal diffusion in the fluid: That is, for Pr = I, the r ate of diffusion of momentum and energy are equal which means that t he calculated temperature and velocity fields will be Similar, the thickness of the momentum and thermal boundary layers will be equal. For Pr <<I (in case of liquid metals), the thickness of the thermal boundary layer will be much more than the thickness of the momentum boundary layer and vice versa. The product of Grashof and Prandtl number is called Rayleigh number. Or, Ra = Gr × Pr.

