Continuous Time Fourier Transform:
The Fourier expansion coefficient x[k] ( in ak OWN) of a periodic signal is
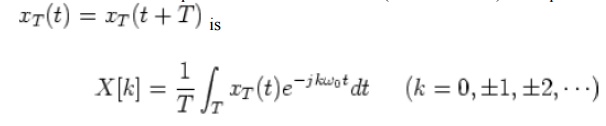
and the Fourier expansion of the signal is:
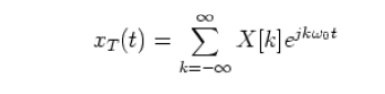
which can also be written as:
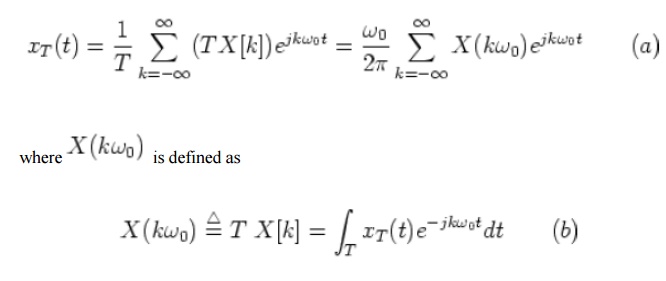
When the period of xT(t) approaches infinity, T->(infinity) the periodic signal xT(t) becomes a non-periodic signal and the following will result:
Interval between two neighboring frequency components becomes zero:
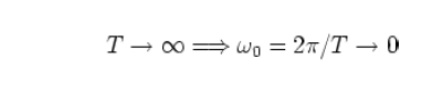
Discrete frequency becomes continuous frequency:

Summation of the Fourier expansion in equation (a) becomes an integral:
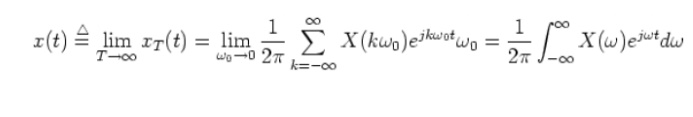
the second equal sign is due to the general fact:
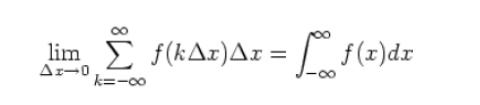
Time integral over in equation (b) becomes over the entire time axis:
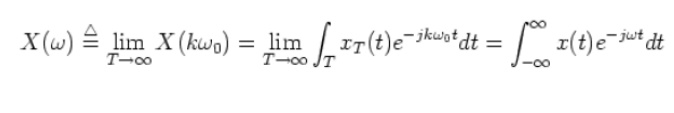
In summary, when the signal is non-periodic x(t)=limT->infxT(t) the Fourier expansion becomes Fourier transform. The forward transform (analysis) is:
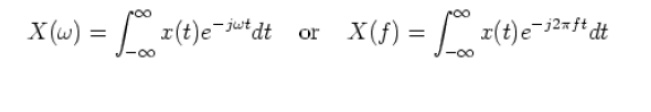
and the inverse transform (synthesis) is:
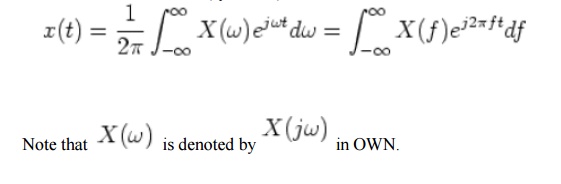
Comparing Fourier coefficient of a periodic signal xT(t) with Fourier spectrum of a non-periodic signal x(t)
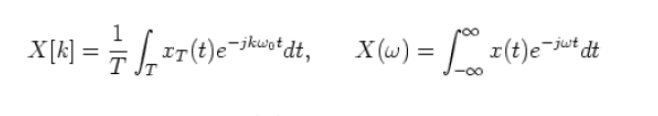
we see that the dimension of X(ω) is different from that of X[k]:

x(t) distributed along the frequency axis. We can only speak of the energy contained in a particular frequency band ω1< ω< ω2

