FREQUENCY TRANSFORMATIONS
INTRODUCTION
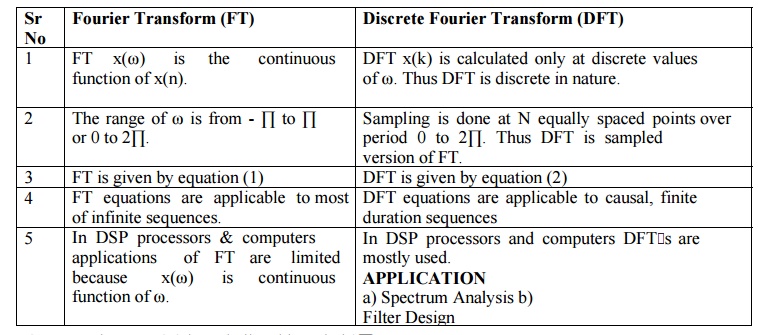
Any signal can be decomposed in terms of sinusoidal (or complex exponential) components. Thus the analysis of signals can be done by transforming time domain signals into frequency domain and vice-versa. This transformation between time and frequency domain is performed with the help of Fourier Transform(FT) But still it is not convenient for computation by DSP processors hence Discrete Fourier Transform(DFT) is used.
Time domain analysis provides some information like amplitude at sampling instant but does not convey frequency content & power, energy spectrum hence frequency domain analysis is used.
For Discrete time signals x(n) , Fourier Transform is denoted as x(ω) & given by

DIFFERENCE BETWEEN FT & DFT
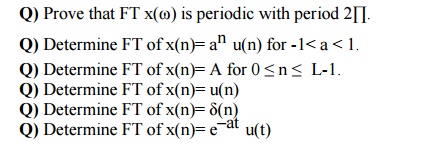
CALCULATION OF DFT & IDFT
For calculation of DFT & IDFT two different methods can be used. First method is using mathematical equation & second method is 4 or 8 point DFT. If x(n) is the sequence of N samples then consider WN= e – j2 ∏ / N (twiddle factor)
Four POINT DFT ( 4-DFT)


EIGHT POINT DFT ( 8-DFT)
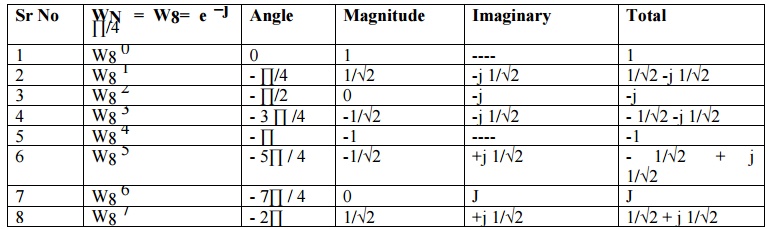
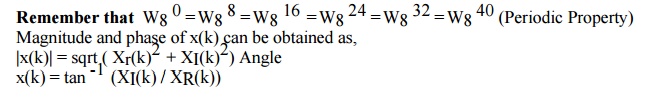
Examples:
Q) Compute DFT of x(n) = {0,1,2,3} Ans: x4=[6, -2+2j, -2, -2-2j ]
Q) Compute DFT of x(n) = {1,0,0,1} Ans: x4=[2, 1+j, 0, 1-j ]
Q) Compute DFT of x(n) = {1,0,1,0} Ans: x4=[2, 0, 2, 0 ]
Q) Compute IDFT of x(k) = {2, 1+j, 0, 1-j } Ans: x4=[1,0,0,1]
DIFFERENCE BETWEEN DFT & IDFT


