Image Enhancement: Spatial domain methods:
Suppose we have a digital image which can be represented by a two dimensional random field A’y ^ . t r
An image processing operator in the spatial domain may be expressed as a mathematical function L applied to the image f to produce a new image -v^ “ ^ ^ 'X' -v^ - as follows.
g{x,y) = T\{x,y)_
The operator T applied on f ( x , y) may be defined over:
A single pixel (x,y) . In this case T is a grey level transformation (or mapping) function.
Some neighbourhood of ( x , y).
T may operate to a set of input images instead of a single image.
Example 1
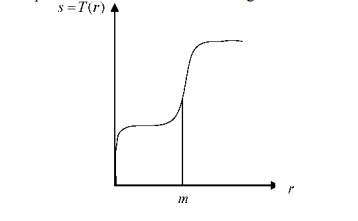
The result of the transformation shown in the figure below is to produce an image of higher contrast than the original, by darkening the levels below m and brightening the levels above m in the original image. This technique is known as contrast stretching.
Example 2
The result of the transformation shown in the figure below is to produce a binary image. s = T(r)
Frequency domain methods
Let g( x, y) be a desired image formed by the convolution of an image f (x, y) and a linear, position invariant operator h(x,y), that is:
g(x,y) = h(x,y)2f(x,y)
The following frequency relationship holds:
G(u, i’) = H (a, v)F(u, i’) We can select H (u, v) so that the desired image
g(x,y) = 3_ 1 i$(ii,v)F(u,v)
exhibits some highlighted features of f (x,y) . For instance, edges in f (x,y) can be accentuated by using a function H(u,v) that emphasises the high frequency components of F(u,v)

